Analisis Komponen Utama (PCA)
- Paham Statistika
- Jan 28, 2022
- 9 min read
Updated: Feb 4, 2022
Principal component analysis (PCA) atau dikenal juga dengan analisis komponen utama merupakan salah satu teknik dalam statistika yang digunakan dalam menangani data besar. Dalam blog kali ini, penulis ingin membagikan informasi yang diharapkan mampu memberikan gambaran abstrak mengenai PCA. (Ditulis oleh HN Rizka, Januari 2022)
"In our lust for measurement, we frequently measure that which we can rather than that which we wish to measure... and forget that there is a difference." - George Udny Yule
PCA hingga saat ini dikenal sebagai teknik yang menyederhanakan permasalahan pada data besar. Secara sederhana PCA merupakan teknik untuk mengurangi redundancy variabel dalam data. Redundancy ini dapat diilustrasikan sebagai berikut
Misalkan anda ingin meneliti produk domestik bruto (PDB) indonesia tahun 2021. Dalam meneliti PDB, terdapat banyak data yang merupakan indikator dalam PDB seperti tingkat pengangguran, tingkat inflasi, neraca sosial-ekonomi, ekspor-impor, dan sebagainya. Selain itu, anda juga dapat menggunakan data PDB tahun-tahun sebelumnya. Anda juga dapat mengumpulkan data harga saham, jumlah IPO yang terjadi dalam setahun, dan berapa banyak CEO yang tampaknya mengajukan tawaran untuk jabatan publik. Dari ilustrasi diatas, terlihat bahwa variabel atau ukuran yang dapat anda gunakan untuk meneliti sangatlah banyak. Dalam menganalisis data dengan banyak variabel tersebut, tentu akan muncul permasalahan. Daiantara masalah yang mungkin muncul adalah hubungan antar variabel-variabel tersebut dan Overfitting.
Permasalahan dalam variabel-variabel yang saling berhubungan ini dapat dicontohkan seperti pada kasus regresi berganda yaitu kasus multikolinearitas. Ketika variabel-variabel prediktor dalam regresi memiliki multikolinearitas, solusi statistik cenderung tidak stabil yang tentunya berdampak pada interpretasi akhir analisis.
Kasus overfitting adalah ketika dalam melakukan analisis statistika, hasil dari estimasi terlalu serupa dengan data asli. Ketika ini terjadi, esensi statistika dalam mempelajari populasi tidak tercapai. Untuk lebih detailnya dapat anda lihat di Overfitting.

Kegunaan PCA
Mungkin dalam keadaan seperti yang diilustrasikan sebelumnya, anda bertanya "mengapa tidak fokus saja ke beberapa variabel yang penting". Istilah mengurangi variabel seperti ini dikenal dengan mengurangi dimensi data. Dalam mengurangi dimensi, terdapat dua cara yaitu eliminasi dan ekstraksi.
Prosedur eliminasi mengurangi variabel dengan hanya menyisihkan variabel yang tidak diinginkan. Seperti pada kasus PDB sebelumnya, pengurangan dimensi dengan eliminasi dapat dilakukan dengan misal hanya mengikutsertakan data-data PDB tahun sebelumnya. Hal ini tentu memiliki kelemahannya yaitu kita tidak secara langsung mengurangi jumlah informasi. Maka dari itu, prosedur ekstraksi menjadi alternatif masalah ini.
Prosedur ekstraksi dilakukan dengan menerapkan aljabar pada data. Secara sederhana, dalam matematika dan statistika, variabel dalam data dipandang sebagai dimensi sehingga penanganan dalam "mengurangi" banyaknya variabel dapat didekati secara aljabar. Lebih tepatnya menggunakan metode dekomposisi dalam aljabar.
Dalam mengeliminasi variabel, PCA melakukan transformasi terlebih dahulu pada data. Transformasi ini bertujuan untuk membangun "data baru" dimana isinya merupakan variabel-variabel yang mengandung seluruh informasi dari data asli. Keistimewaan dari data baru ini adalah variabel-variabel didalamnya merupakan hasil kombinasi dari variabel-variabel asli. Setiap variabel dalam data baru memiliki sebagian dari informasi keseluruhan dalam data asli. Selain itu, tingkat informasi yang dikandung dalam variabel baru menjadi dasar urutannya dalam data baru. Sehingga, pemilihan variabel baru yang digunakan dapat langsung ditentukan berdasarkan persentase informasi yang ingin dipertahankan dari data asli.
Kapan PCA Digunakan?
Untuk menjawab pertanyaan diatas, bayangkan anda telah selesai mengidentifikasi penelitian yang ingin anda lakukan ( contoh : prediksi PDB Indonesia tahun 2022 ). Kemudian kumpulkan data terkait yang menurut anda dapat membantu menyelesaikan permasalahan penelitian. Setelah itu, tanyakan pertanyaan berikut kepada diri anda :
Apakah anda ingin mengurangi banyaknya variabel bebas namun tidak dapat mengidentifikasi secara pasti variabel mana yang harus anda hilangkan?
Apakah anda ingin memastikan variabel bebas penelitian tidak saling bergantung/berhubungan?
Apakah anda tidak masalah jika variabel bebas anda kurang dapat diinterpretasikan?
Untuk semua pertanyaan diatas, jika anda menjawab "ya", PCA merupakan solusi yang baik.
Penjelasan yang telah diberikan diatas merupakan penjelasan dasar dari PCA dan tujuannya, bagi anda yang memiliki ketertarikan lebih dan memiliki setidaknya pemahaman mengenai aljabar linear dasar, saya sarankan untuk melihat diskusi mengenai hubungan PCA dengan nilai eigen berikut : Making sense of PCA and Eigen. Bahasan selanjutnya akan memerlukan pemahaman pembaca yang nyaman dengan materi dalam topik aljabar linear dasar dan dasar-dasar statistika.
Metode Dasar dalam PCA
Sebelum masuk ke prosedur penerapan PCA, penulis ingin memebahas beberapa istilah yang akan digunakan.
Matriks Kovarian dan Korelasi
Matriks kovarian merupakan matriks yang berisi variansi dan kovariansi. Tentunya matriks ini berkorespondensi dengan data. Sebagai contoh misalkan terdapat suatu data dengan 3 variabel (variabel x, y, dan z), maka bentuk matriks kovariannya adalah sebagai berikut :

Matriks korelasi serupa dengan matriks kovarian hanya saja berisi korelasi. Diagonal utama berisi bilangan "1" dan pada posisi lain merupakan korelasi antar variabel.
Dekomposisi Matriks
Didalam aljabar linear, dekomposisi matriks merupakan faktorisasi matriks kedalam bentuk perkalian matriks-matriks. Terdapat beberapa metode yang digunakan dalam melakukan dekomposisi matriks seperti dekomposisi Cholesky, akar kuadrat, dan nilai singular (SVD).
Cara Kerja PCA
Dalam menerapkan PCA, tentunya diperlukan acuan prosedur. Untuk bagian ini, penulis membahas secara garis besar prosedur yang dilakukan tanpa teknis matematikanya. Pembahasan yang sedikit lebih teknis dibahas di bagian berikutnya. Secara garis besar prosedur penerapan PCA adalah sebagai berikut :
Siapkan data pengamatan dan identifikasi jenis variabel sedemikian variabel-variabel dikelompokkan menajdi variabel dependen dan independen. Selanjutnya untuk variabel dependen akan dinotasikan dengan Y dan variabel independen dinotasikan dengan X.
Tentukan jenis variabel mana yang ingin anda reduksi dimensinya. Misalkan akan direduksi variabel-variabel independen untuk keperluan prediksi (seperti regresi). Maka matriks yang menjadi target reduksi adalah X dimana ini berisi variabel-variabel independen.
Sekarang bayangkan setiap variabel sebagai dimensi-dimensi dalam suatu ruang. Untuk memudahkan, perhatikan grafik berikut :

Dari gambar diatas, terlihat bahwa dua variabel akan membentuk ruang dua dimensi. Perumum ini menjadi ruang dimensi n, dimana n adalah banyaknya variabel anda. Visualisasi tentu terbatas pada tiga dimensi, namun secara teori ini bukanlah hal yang baru.
Dari ilustrasi diatas, terlihat bahwa data memilki "arah" dan ini direpresentasikan dengan garis hijau dan merah. Sekarang perhatikan persebaran titik pengamatan dan bandingkan dengan kedua garis tersebut. Jelas bahwa persebaran titik-titik cenderung "besar" di arah garis merah. Secara esensial, melebarnya data di arah garis merah mengimplikasikan "variansi" yang tinggi diarah tersebut. Hal inilah yang akan ditangkap sebagai "informasi" dalam PCA.
Prosedur selanjutnya yang dilakukan PCA adalah melakukan transformasi data. Ini dilakukan dengan bantuan metode dekomposisi matriks nilai singular. Secara visual, transformasi ini diibaratkan seperti kita melihat data dari perspektif lain sedemikian data "sejajar" dengan arah dominan (dalam contoh sebelumnya arah dominannya adalah garis merah).
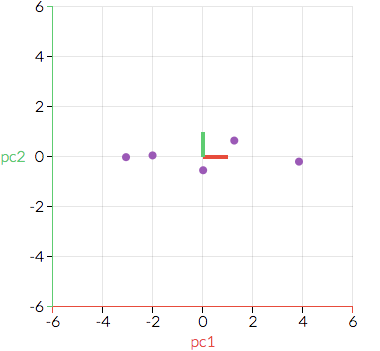
Gambar diatas merupakan hasil transformasi PCA. Secara esensial, tidak ada perubahan nilai. Yang dilakukan hanyalah mengganti perspektif. Dalam contoh ini hanya terdapat dua variabel yang tentunya bukan data besar. Untuk penerapan pada data besar, ketika dimensi yang ada sangat banyak, maka kita akan "memampatkan" data sedemikian kita hanya memperhatikan dimensi-dimensi yang dominan. Pemampatan ini dapat diilustrasikan dengan contoh sebelumnya dengan cara memproyeksikan ke satu dimensi. Hasilnya kira-kira akan terlihat seperti berikut :

Algoritma Kerja PCA
Pada bagian dijelaskan secara garis besar teknis algoritma penerapan PCA. Pembahasan didasarkan pada ilustrasi sebelumnya.
Setelah memastikan dan mengidentifikasi data yang akan direduksi dimensinya lakukan standardisasi. Caranya adalah dengan menghitung rata-rata/mean dan standar deviasi dari masing-masing variabel. Kemudian untuk setiap pengamatan, kurangi dengan mean tersebut lalu bagi dengan standar deviasi. Prosedur ini secara matematis dapat dituliskan sebagai berikut : misalkan X1_n adalah nilai variabel ke-n untuk pengamatan 1 [bayangkan seperti X1 adalah mahasiswa 1 dan ukuran yang direkam adalah tinggi badan dan berat badan, maka X1 = (tinggi badan1, berat badan1)] maka standardisasi untuk variabel ke-k pada pengamatan 1 adalah : (X1_k - mean_k)/(standar.deviasi_k).
Notasikan data yang telah distandardisasi sebagai Z. Kalikan transpos matriks data Z dengan matriks data Z [dapat dituliskan sebagai Z* = (Z^t)Z, dimana (Z^t) adalah transpos matriks Z].
Lakukan dekomposisi eigen pada matriks Z* sehingga didapatkan matriks faktor PD(P^-1). Lakukan pengurutan pada matriks faktor tersebut sedemikian terurut berdasarkan nilai eigen terbesar, pastikan vektor eigen juga berubah mengikut nilai eigen yang berkorespondensi. Ambil matriks P* yang merupakan matriks faktor P yang telah terurut berdasarkan nilai eigen terbesar.
Hitung Z** = ZP* dan telah didapatkan matriks data baru hasil transformasi PCA. Sebagai tambahan setiap kolom/variabel baru di matriks data Z** adalah saling bebas linear. Selain itu, istilah yang digunakan untuk variabel-variabel baru ini dikenal dengan "komponen".
Prosedur terakhir adalah menentukan berapa banyak komponen yang ingin dipertahankan. Beberapa cara diantaranya adalah :
Berdasarkan kemampuan visualisasi sehingga hanya terbatas untuk mempertahankan hingga 3 variabel.
Berdasarkan tingkat total variansi yang dijelaskan, hal ini diilustrasikan pada bagian sebelumnya mengenai persebaran data di komponen sehingga metode ini mempeertahankan komponen-komponen yang mengandung bagian variansi terbesar hingga mencapai tingkat tertentu (misal ditetapkan bahwa ingin dipertahankan 80% total variansi dijelaskan pada data dengan 12 komponen. Pada 3 komponen pertama telah terkandung 82% total variansi dijelaskan, maka diputuskan hanya 3 komponen pertama yang dipertahankan).
Metode yang dikenal dengan elbow yaitu mirip dengan metode kedua namun daripada menetapkan tingkat tertentu, peneliti menilai secara subjektif hingga komponen mana tingkat total variansi yang dijelaskan tidak bertambah secara signifikan (mialkna terdapat 12 komponen dengan komponen 1 dan 2 memiliki masing-masing 35% dan 30%. Sisa tingkat variansi dijelaskan adalah 35% dengan komponen 3 hanya mengandung 6% sehingga diputuskan bahwa hanya komponen 1 dan 2 yang dipertahankan).
Terkait total variansi dijelaskan, penghitungan ini didasarkan pada nilai eigen.
Setelah membahas mengani PCA secara garis besar dalam blog ini, harapan penulis adalah pembaca yang sebelumnya kurang terlalu memahami proses bekerja PCA menajdi sedikit lebih memahaminya. Selanjutnya, penulis ingin membagi contoh penerapan PCA pada data asli. Data dapat anda download di link berikut : Data klien.
Analisis Data Klien
Data yang akan dianaisis merupakan data klien kartu kredit bank, beberapa variabel diantaranya adalah Limit_BAL adalah jumlah kredit yang diberikan, Pay_ yaitu status pembayaran kembali di periode-periode sebelumnya, Bill_ yaitu total jumlah tagihan, dan Pay_AMT adalah jumlah pemabayaran sebelumnya. Tujuan penelitian kali ini adalah untuk melakukan prediksi untuk status pembayaran selanjutnya dari klien. Hal ini dilakukan untuk mengantisipasi klien yang akan mangkir dalam membayar pada setidaknya satu kali tagihan selama 6 bulan kedepan. Analisis dilakukan dengan bantuan software R. Untuk kode lengkap analisis dapat anda lihat di github penulis pada repositori multivariate_analysis dengan judul PCA.
Untuk meneliti data ini, penulis hanya akan menggunakan variabel Bill_, dan Pay_AMT. Hal ini dilakukan untuk menyesuaikan kebutuhan saat ini yaitu memberikan contoh penerapan PCA pada data asli. PCA diperuntukkan untuk variabel numerik kontinu. Sedangkan ketika melakukan reduksi dimensi pada variabel kategorik, anda dapat menggunakan analisis korespondensi/correspondence analysis (CA). Penulis juga tertarik untuk membahas metode tersebut di masa mendatang.
Setelah memutuskan variabel penelitian, selanjutnya dilakukan persiapan awal yaitu pemisahan data training dan test. Hal ini dilakukan untuk memisahkan peran data yang akan digunakan untuk analisis (training) dan data yang digunakan sebagai tujuan prediksi (test). Data yang telah anda download telah memisahkan kedua data tersebut.
Setelah data siap, selanjutnya dapat dimulai transformasi variabel dengan PCA. Dengan menggunakan software R, hasil transformasi data dapat langsung dikeluarkan. Berikut adalah 7 pengamatan pertama dari data training pada komponen PCA yang didapatkan :

Selanjutnya akan ditentukan berapa komponen yang akan dipertahankan. Penulis tidak ingin menentukan ini berdasarkan persentase. Hal ini dikarenakan semakin banyak variabel penelitian, mempertahankan tingkat variansi dijelaskan tertentu akan membutuhkan banyak variabel. Maka dari itu penulis memutuskan untuk menggambarkan scree plot persentase variansi dijelaskan terlebih dahulu. Hasilnya adalah sebagai berikut :
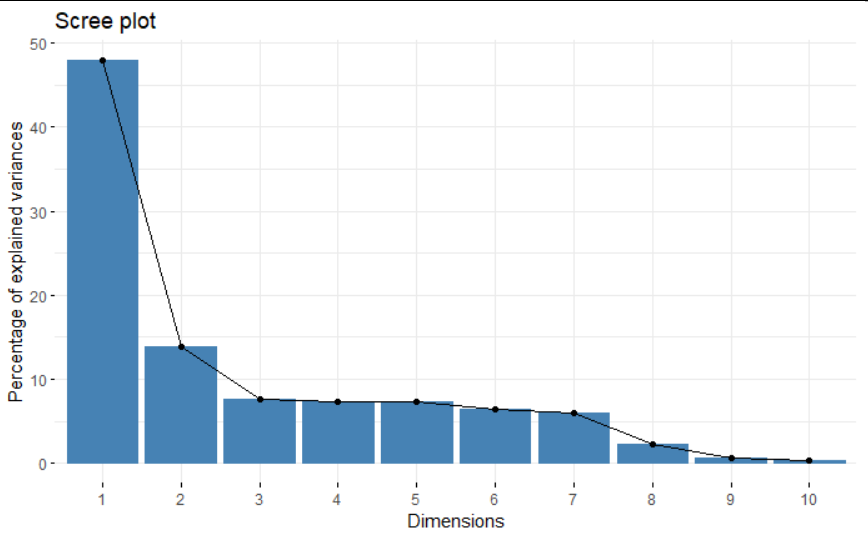
Dari plot diatas, didapatkan bahwa komponen/dimensi 1 dan 2 telah mengakumulasi lebih dari 60% dari total variansi dijelaskan. Dengan kata lain, dengan hanya mempertahankan 2 komponen baru, kita mempertahankan lebih dari 60% informasi dari data. Tentu ini sangatlah berguna karena selain kita dapat melakukan visualisasi data ke dimensi 2, informasi yang dipertahankan dari data asli masih cukup besar. Tentu anda dapat mempertahankan lebih dari 2 komponen, namun anda akan menukar tambahan tingkat informasi tersebut dengan kesederhanaan dan kemampuan untuk merepresentasikan data dalam plot.
Dengan mempertahankan 2 dimensi pertama, kita selanjutnya dapat melakukan analisis kontribusi individual dan variabel terhadap dimensi baru. Analisis kontribusi ini dapat kemudian digunakan untuk melakukan prediksi. Plot-plot berikut merupakan kontribusi yang diberikan individu dan variabel untuk 2 dimensi pertama PCA :
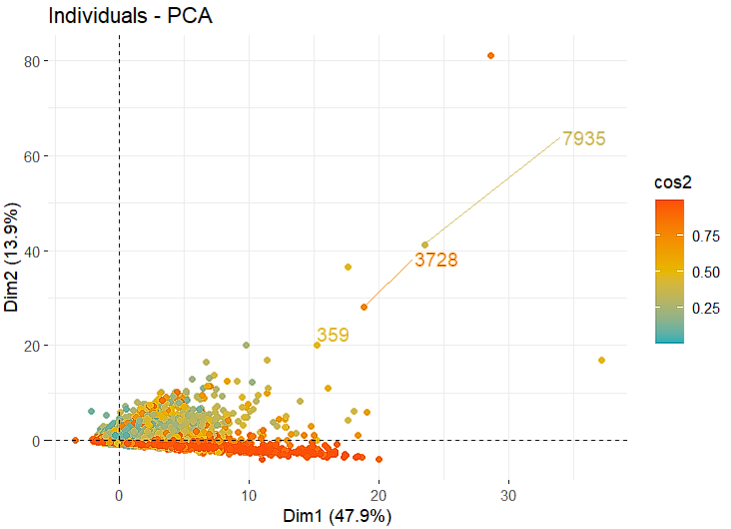

Pada plot individu untuk kasus ini tidak terlalu memberikan informasi ataupun dapat digunakan. Karena metode yang digunakan untuk menganalisis kali ini termasuk kedalam supervised learning . Ketika berhadapan dengan metode unsupervised plot individu tersebut dapat digunakan. Untuk plot variabel, informasi yang dapat disimpulkan adalah : (1) dimensi pertama merupakan dimensi yang mayoritas informasinya datang dari Bill_AMT dan secara tidak langsung kita dapat mengatakan bahwa dimensi pertama adalah informasi mengenai jumlah tagihan; (2) serupa dengan poin 1, untuk dimensi kedua merupakan informasi dari variabel-variabel jumlah pembayaran; (3) secara keseluruhan, mayoritas informasi ruang dua dimensi ini dikontribusi oleh Bill_AMT.
Setelah mendapatkan transformasi PCA berdasarkan data training diatas, transformasi yang sama dilakukan pada data test. Dengan melakukan PCA untuk masalah ini, kita telah menyederhanakan data dengan total 23 variabel independen/prediktor menjadi 13 prediktor. Sehingga data yang akan diprediksi berubah menjadi seperti contoh 7 pengamatan pertama berikut :
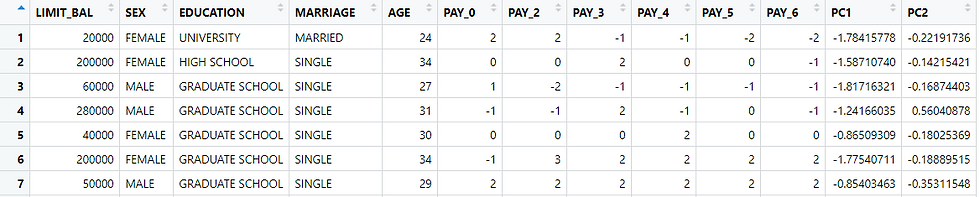
Tentu 13 prediktor diatas tidak perlu digunakan semuanya. Untuk menentukan variabel yang berguna dalam prediksi status pembayaran klien, digunakan model regresi logistik. Karena blog ini tidak membahas mengenai model ini, penulis melewati bagian ini dan hanya menceritakan gambaran kasar abstraknya.
Menggunakan data training, dibangun model regresi logistik. Sebelum membangun model, penulis memutuskan untuk tidak memasukkan variabel-variabel Pay_ sebagai prediktor karena menurut penulis prediktor ini kurang relevan jika diteliti diluar konteks analisis time series atau runtun waktu. Sehingga data training yang digunakan untuk membangun model regresi logistik terlihat seperti contoh berikut :
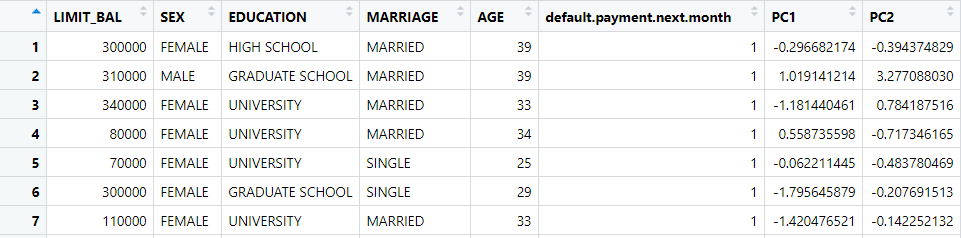
Setelah membangun model regresi logistik, didapatkan hasil bahwa selain dari komponen PCA, Limit_BAL atau jumlah kredit yang diberikan, Education atau level pendidikan Marriage atau status perkawinan signifikan mempengaruhi status pembayaran selanjutnya. Dalam memprediksi menggunakan regresi logistik, hasil prediksi dievaluasi menggunakan ukuran specificity dan sensitivity. Dari hasil analisis dengan data training klien didapatkan specificity dan sensitivity prediksi optimum mencapai 61,8%.
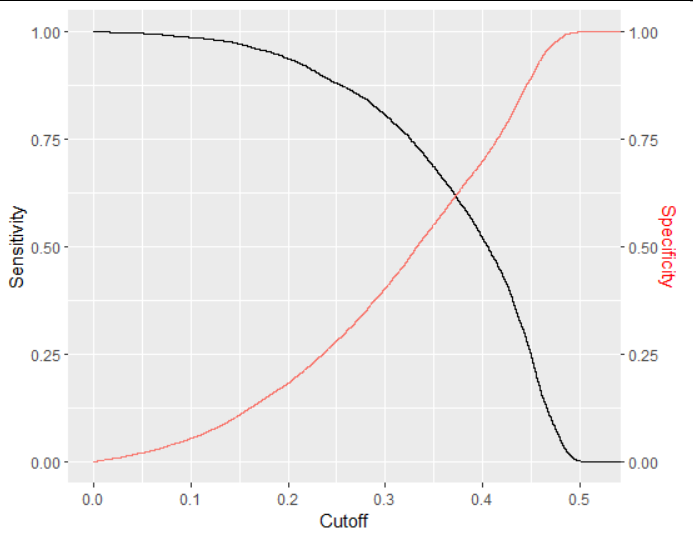
Setelah menyelesaikan model dan mendapatkan cutoff optimum, prosedur terakhir adalah menerapkan model tersebut pada data test. Sehingga didapatkan prediksi pada 6000 klien mengenai apakah individu didalamnya akan mangkir dari pembayaran kredit setidaknya satu kali selama periode 6 bulan kedepan. Data test yang diprediksi dan hasil prediksinya hasilnya adalah seperti berikut :

Analisis yang telah dilakukan dapat anda coba dan replikasi sendiri menggunakan kode di github penulis : Github/hakiimnurrizka . Penerapan hasil PCA tentunya tidak terbatas pada prediksi atau metode supervised seperti yang telah dicontohkan. Ini hanya bertujuan untuk memberikan salah satu contoh penggunaan hasil PCA.

Comments