Analisis Data Kategorik
- Feb 17, 2022
- 7 min read
Metode analisis data kategorik menjadi semakin banyak digunakan semenjak pertengahan abad ke-20. Blog kali ini akan membahas beberapa metode analisis data kategorik yang banyak digunakan. (Ditulis oleh HN Rizka, Februari 2022)
"research does not assure definite rewards, but it assures lesser risk" -Amit Kalantri
Pembaca pasti setidaknya pernah menemui atau melihat grafik yang menampilkan data yang memperlihatkan jumlah atau proporsi kelompok individu tertentu. Contoh mungkin seperti di Puskesmas, penulis pernah melihat poster mengenai "Proporsi meninggal akibat beberapa jenis penyakit". Di poster tersebut terdapat perbandingan persentase untuk memperlihatkan seberapa berbeda tingkat kematian akibat penyakit-penyakit seperti demam berdarah, malaria, dan thypus. Beberapa poster serupa juga terpajang didekat poster tersebut. Penulis kemudian bertanya dalam benak diri sendiri "mengapa hanya memunculkan angka perbandingan untuk satu variabel saja?". Mengapa tidak memaparkan, misalnya asosiasi antara konsumsi rokok dengan ekspektasi lama hidup. Atau memberikan interpretasi pada hubungan antara kegemukan dengan resiko penyakit seperti serangan jantung secara statistik. Hal ini karena masih kurangnya paparan mengenai metode analisis untuk data kategorikitu sendiri dan anggapan umum bahwa statistika untuk data kategorik masih sulit diterapkan.
Metode Analisis Data Kategorik
Tipe data selain numerik dapat berupa pengelompokan atau pelabelan yang sering dikenal dengan data kategorik. Bentuk dari pelabelan ini juga sangat luas, namun pada prinsipnya data ini bekerja dengan memperhatikan label tiap individu. Contoh pelabelan berdasarkan jenis kelamin dapat berupa : (1) laki-laki dan perempuan, atau (2) 0 dan 1. Kedua tipe pelabelan ini tetaplah berjenis kategorik.
Dalam penanganan data kategorik, diperlukan metode khusus dan dalam salah satu seri buku terkenal oleh Alan Agresti, metode-metode dalam menangani data kategorik dikompilasikan menjadi "Analisis Data Kategorik". Dalam blog kali ini, akan dibahas beberapa metode analisis data kategorik berdasarkan package di software R : vcd. Beberapa metode yang dibahas adalah : tabel silang frekuensi, independensi antar variabel, model loglinear, plot mosaik, dan model prediksi dengan variabel kontinu.
Visualisasi Data Kategorik
Pertama, mari kita persiapkan data kita. Digunakan data klien yang telah digunakan di blog-blog sebelumnya. Sebagai konteks dna pengingat kembali, data ini digunakan dalam salah bentuk analisis probabilitas default. Sederhananya, dilakukan karakterisasi data untuk memprediksi klien-klien yang berpotensi untuk mangkir pembayaran kreditnya. Dalam blog ini, akan difokuskan ke variabel-variabel berikut :

Terkait variabel PAY_, penulis merasa bahwa banyaknya level/kategori terlalu banyak/redundant. Maka dari itu dilakukan pendefinisian kategori dengan : -1 untuk tidak pernah melewatkan pemabayaran, 0 adalah pembayaran sebagian, dan 1 untuk yang pernah melewatkan pembayaran. Didapatkan struktur data sebagai berikut :

Dari data ini, dapat ditampilkan beberapa jenis grafik untuk setiap variabelnya. Seperti contoh berikut :



Dapat juga dilakukan plotting untuk 2 variabel sekaligus seperti berikut :

Selanjutnya, ditampilkan bentuk data dalam beberapa jenis tabel.
Tabel Frekuensi dan Tabel Silang
Tabel frekuensi menyatakan banyaknya individu yang masuk dalam kategori tertentu. Misalkan pada tabel frekuensi berikut :
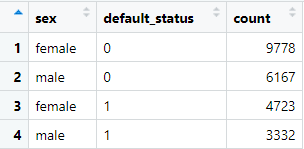
Dalam tabel diatas, dapat dilihat per baris, kemudian pada kolom "count" menyatakan banyaknya individu yang termasuk dalam kategori baris tersebut. Baris pertama menyatakan individu dengan jenis kelamin wanita (female) dengan status default tidak pernah mangkir bayar (0) sebanyak 9778 individu. Yang dapat dianalisis pada tabel frekuensi dengan 2 variabel seperti adalah proporsinya. Seperti contoh : untuk jenis kelamin wanita, proporsi individu default adalah 4723/(4723+9778) = 32.6% sedangkan untuk jenis kelamin pria proporsi individu defaultnya adalah 3332/(3332+6167) = 35%. Tentu ini dapat dilakukan pada prediktor-prediktor lainnya.

Bentuk tabel frekuensi juga dapat berupa matriks seperti berikut :

Tabel seperti diatas juga dikenal dengan tabel silang. Selain melakukan tabulasi dengan 2 variabel diatas, kita juga dapat melakukan tabulasi silang untuk 3 variabel.
Tabulasi silang 3 variabel menjadi perhatian ketika terdapat kecurigaan asosiasi antara 2 variabel yang dimoderasi oleh variabel ketiga. Konsep moderasi ini sebenarnya lebih ke tingkat lanjutan. Untuk memberikan gambaran, perhatikan ilustrasi berikut :
Anda ingin meneliti tingkat stress orang yang dicurigai sangat mempengaruhi kesehatan. Setelah mendapatkan data penelitian, anda menemukan bahwa efek tingkat stress pada kesehatan cenderung lebih kuat pada individu dengan jenis kelamin pria. Dalam kasus ini, jenis kelamin tersebut seakan "menengahi" efek tingkat stress terhadap kesehatan seseorang. Sehingga selain dari variabel tingkat stress dan status kesehatan seseorang, anda juga mempertimbangkan variabel jenis kelamin dalam penelitian anda.Kembali ke permasalah pada status pembayaran klien sebelumnya, kita bisa mencurigai adanya penengah yang menyebabkan tingkat default pria lebih besar daripada perempuan. Perhatikan tabel berikut :

Perhatikan untuk kategori "married" dan "single". Untuk status "married" proporsi klien wanita yang default adalah 2263/(2263+4497) = 33.5% sedangkan proporsi klien pria yang default adalah 1407/(1407+2725) = 34%. Pada status "single" proporsi klien wanita yang default adalah 2263/(2263+4497) = 31.5% sedangkan proporsi klien pria yang default adalah 1407/(1407+2725) = 36%. Terlihat bahwa perbedaan proporsi keduanya berbeda-beda tergantung pada status pernikahan.
Melakukan eksplorasi data dengan tabel silang seperti diatas dapat memberikan gambaran besar mengenai asosiasi antar variabel yang mungkin terjadi. Untuk memastikan asosiasi ini tentunya dapat dilakukan melalui uji hipotesis.
Uji Independensi
Uji selanjutnya merupakan bagian dari uji hipotesis untuk memastikan apakah asosiasi antar variabel memang signifikan. Seperti contoh pada bagian sebelumnya, dapat dicurigai adanya hubungan antara jenis kelamin dengan status default.

Hasil diatas menunjukkan bukti yang kuat adanya asosiasi antara jenis kelamin dengan status default seseorang. Untuk melihat asosiasi antar kategorinya, kita dapat menggunakan matriks korelasi residual berikut :

Dari gambar diatas, terlihat bahwa asosiasi positif yang kuat muncul pada jenis kelamin pria dan pembayaran yang default. Dengan kata lain, klien dengan jenis kelamin pria cenderung memiliki asosiasi yang kuat dengan "mangkir dari pembayaran kredit".
Hal serupa juga ditemukan pada variabel tingkat pendidikan, dimana ditemukan hubungan signifikan antara tingkat pendidikan terhadap status default klien. Untuk asosiasi setiap kategorinya sendiri adalah sebagai berikut :

Asosiasi positif tertinggi dengan status klien yang default muncul pada kategori pendidikan SMA, sedangkan asosiasi negatif terbesar dengan "mangkir pembayaran kredit" ada pada jenis pendidikan "lainnya". Pada variabel status pernikahan, tidak ditemukan bukti yang kuat adanya asosiasi dengan status default klien.
Selain uji 2 arah seperti contoh diatas, dapat dilakukan uji independensi 3 arah. Interpretasi pengujian 3 arah mirip seperti logika moderasi sebelumnya. Dengan kata lain, asosiasi antara 2 variabel dapat "ditengahi" oleh variabel lain. Uji ini juga dikenal dengan uji independensi bersyarat : Mantel-Haenszel. Seperti contoh : asosiasi antara jenis kelamin dengan status pembayaran ketika disesuaikan dengan status pernikahan.

Dari hasil diatas didapatkan bahwa asosiasi antara jenis kelamin dan status pembayaran klien yang dikondisikan dengan status pernikahan adalah signifikan. Lalu apa perbedaan pengujian ini dengan sebelumnya? Ini terkait dengan bagaimana kita menangani data tersebut. Pada kasus sebelumnya, kita seolah-olah hanya menganalisis asosiasi 2 variabel dan mengabaikan variabel lainnya untuk setiap pengujian. Pada kasus 3 variabel ini, kita sebenarnya juga menganalisis asosiasi antara 2 variabel namun kita mempertimbangkan 3 variabel secara bersama. Hal ini sesuai dengan ilustrasi tingkat stress sebelumnya.
Untuk melihat tingkat asosiasi antara jenis kelamin dengan status pembayaran yang berdasarkan status pernikahan dapat digunakan odds ratio berikut :

Untuk memudahkan interpretasi, kita perhatikan kembali tabel antara jenis kelamin, status pembayaran, dan status pernikahan.

Dengan menggunakan odds ratio diatas dan tabel, didapatkan bahwa pada data :
Odds pada klien wanita untuk tidak pernah mangkir dari pembayaran adalah 1.026 dari klien pria, ketika status pernikahan mereka "married". Dengan kata lain, klien wanita yang telah menikah lebih cenderung berasosiasi dengan status pembayaran non-default dibandingkan klien pria yang telah menikah.
Odds pada klien wanita untuk tidak pernah mangkir dari pembayaran adalah 0.585 dari klien pria, ketika status pernikahan mereka "others". Dengan kata lain, klien pria yang status pernikahannya "others" lebih cenderung berasosiasi dengan status pembayaran non-default dibandingkan klien wanita dengan status pernikahan yang sama.
Odds pada klien wanita untuk tidak pernah mangkir dari pembayaran adalah 1.222 dari klien pria, ketika status pernikahan mereka "single". Dengan kata lain, klien wanita yang status pernikahannya "single" lebih cenderung berasosiasi dengan status pembayaran non-default dibandingkan klien pria lajang.
Dari temuan diatas, saran yang dapat diberikan adalah untuk bank pemberi kredit agar lebih berhati-hati dengan klien pria dengan status pernikahan selain "others" atau latar belakang pendidikan SMA. Hal ini karena asosiasi kedua kategori tersebut cukup tinggi dengan status default atau mangkir pembayaran dari kategori lawannya.
Sebagai penutup sub bagian ini, diterapkan analisis korepsondensi antara tingkat pendidikan dan status pernikahan.

Catatan : analisis korespondensi ekuivalen dengan analisis komponen utama, tentunya untuk variabel kategorik, yaitu untuk mengekstraksi variabel dan melakukan visualisasi di dimensi yang rendah. Pembahasan lebih detail akan ada di blog di mendatang.
Penerapan analisis korespondensi pada variabel tingkat pendidikan dan status pernikahan menghasilkan plot korepondensi sebagai berikut

Plot diatas menunjukkan kedekatan antara status "single" dengan pendidikan "graduate school". Hal ini memberikan gambaran bahwa mayoritas klien dengan status "single" memiliki latar belakang pendidikan pascasarjana. Kedekatan antar kategori lain dapat anda temukan di plot diatas dan tidak terbatas hanya pada kategori antar 2 variabel berbeda. Perluasan analisis korespondensi dapat diterapkan untuk lebih dari 2 variabel kategorik. Namun untuk kali ini, penulis cukupkan sebagai bentuk pengenalan dalam sub bagian independensi antar variabel kategorik blog ini.
Model Loglinear dan Plot Mosaik
Setelah membahas mengenai independensi diatas, kita akan tertarik dengan pertanyaan : bagaimana ketika menganalisis hubungan beberapa variabel kategorik secara bersamaan. Sebelumnya kita telah sedikit mengintip ini dengan melakukan analisis asosiasi 2 variabel bersyarat suatu variabel lain. Representasi untuk asosiasi bersyarat ini adalah : ~A*B+C. A menyatakan variabel 1 yang dianalisis asosiasinya dengan variabel B, C menyatakan variabel syarat. Sekarang bayangkan ketika anda tidak memiliki hipotesis apapun mengenai hubungan antara ketiga variabel, tentu perlu dieksplorasi semua kemungkinan hubungan yang terjadi. Apakah ketiga variabel saling bebas (~A+B+C) atau mungkin terdapat interaksi tiap 2 variabel (~A*B + A*C + B*C) atau bahkan ketiga saling berhubungan bersama-sama (~A*B*C). Model loglinear memberikan solusi untuk mengeksplorasi kemungkinan-kemungkinan ini melalui persamaan linear seperti representasi diatas. Lebih tepatnya, misalkan untuk model yang semua saling bebas (~A+B+C) :

dimana m merupkan nilai harapan frekuensi. Contoh model lain seperti asosiasi antara A dan B namun independen terhadap C (~A*B+C) :

Untuk 3 variabel, berikut adalah model loglinear yang mungkin terjadi :

Selanjutnya diterapkan model loglinear untuk menganalisis hubungan ketiga variabel prediktor pada data klien : Jenis kelamin, tingkat pendidikan, dan status pernikahan. Untuk model saling bebas keseluruhan memiliki statistik berikut :

secara individu statistik ini memang tidak terlalu berguna, namun statistik likelihood ratio daapt digunakan untuk menentukan apakah bagian dari model loglinear perlu dipertahankan. Konsep ini mirip seperti seleksi variabel pada model regresi. Perbedaannya seperti istilah full model di regresi yang ekuivalen dengan saturated model di loglinear. Selain itu, tentunya dari segi statistik yang digunakan : error pada regresi dan deviance pada loglinear. Kembali ke pokok bahasan sebelumnya, dengan mengajukan beberapa model, kita dapat tentukan manakah model yang terbaik untuk merepresentasikan hubungan 3 variabel prediktor pada data klien. Didapatkan hasil sebagai berikut :

Anda dapat melakukan backward ataupun forward selection untuk memilih model, pada akhirnya model penuh atau saturated (~A*B*C) merupakan model terbaik. Dengan kata lain ketiga variabel prediktor tersebut saling berhubungan atau berasosiasi secara bersamaan. Untuk lebih menampilkan hasil fit model loglinear, dapat dilakukan plotting mosaic seperti berikut :

Contoh hal yang bisa didapatkan dari plot diatas adalah klien dengan latar belakang pendidikan pasca sarjana didominasi oleh pria yang sudah menikah dan diikuti oleh wanita lajang.

Comments