Regularisasi
- Paham Statistika
- Feb 8, 2022
- 4 min read
Metode dalam menangani overfitting model pada machine learning. Metode cukup baik karena model yang didapatkan cenderung lebih robust terhadap perubahan pada data. (Ditulis oleh : HN Rizka, Februari 2022).
"The greatest strategy is doomed if implemented badly" -Bernhard Riemann
Regularisasi pada Regresi Linear
Dalam blog tepat sebelum ini, terdapat satu metode dengan nama yang mirip dengan judul blog kali ini. Regularized, ya kata yang sepertinya mengimplikasikan bahwa suatu objek yang dirujuknya diubah menjadi suatu yang terkesan "biasa". Dalam machine learning (ML) regularisasi merupakan salah satu konsep dasar yang sangat berguna untuk mengatur model sedemikian hasil yang didapatkan memiliki kesalahan atau dalam konteks ML dan statistika dikenal dengan error.
Untuk mengurangi error ini, regularisasi diterapkan pada fungsi dalam model. Dalam kasus regresi, misalkan, regularisasi diterapkan pada persamaan regresi. Untuk lebih memberikan ilustrasi perhatikan contoh situasi berikut :
Anda memiliki data pengamatan yang terdiri atas variabel prediktor X = (x1, x2, .., xn) dan variabel tujuan yang berkorespondensi dengan ini Y = (y1, y2, .., yn). Katakan anda telah membangun persamaan yang menghubungkan kedua variabel sebagai y = sin(2πx) + e. Tujuan anda selanjutnya adalah melakukan prediksi untuk nilai-nilai prediktor yang tidak ada di X. Pada keadaan seperti ini, dapat dilakukan estimasi fungsi regresi dengan persamaan polinomial derajat M : y = b0 + b1x + b2x^2 + .. + bMx^MDengan melakukan estimasti fungsi sebenarnya yang menghubungkan X dan Y menggunakan beberapa persamaan polinomial didapatkan hasil sebagai berikut :

Dari hasil diatas terlihat adanya tren bahwa semakin besar derajat persamaan polinomial, data semakin diakomodasi oleh model. Dengan kata lain garis yang terbentuk semakin mendekati pola data. Dalam konteks normal, kita akan tergoda untuk menggunakan model dengan persamaan polinomial derajat tinggi (misalkan derajat M = 9). Tapi sebelum kita mengambil keputusan tersebut, mari kita lihat performa dari tiap model polinomial derajat M = 1 hingga 9 ketika diterapkan pada data yang berbeda dari yang telah digunakan. Dengan kata lain, ini seperti menguji bagaimana performa model dalam melakukan prediksi data baru. Untuk mengukur kualitas performa digunakan mean dari kuadrat selisih antara nilai prediksi dengan nilai sebenarnya, dikenal dengan mean square error (MSE). Nilai MSE yang kecil merupakan hal yang diinginkan dalam model.

Didapatkan hasil sebagai berikut :

Didapatkan bahwa persamaan polinomial dengan performa terbaik pada data baru adalah pada derajat 3. Selain dari MSE, kita juga dapat membandingkan garis fungsi polinomial dengan fungsi sebenarnya yang menghubungkan variabel X dan Y.

Sebagai pengingat, membandingkan dua garis seperti diatas tentunya tidak aplikatif, karena hampir setiap saat kita hanya akan mengetahui titik-titik observasi seperti pada grafik 4 derajat polinomial sebelumnya. Kita dapat membandingkan keadaan ini karena kita melakukan simulasi data dimana kita mengatur struktur data tersebut.Konsep membandingkan performa model pada data baru seperti ini dikenal dengan istilah cross validation. Biasanya untuk melakukan ini, data yang dimiliki dibagi menjadi 2 : data training dan test. Training digunakan untuk membangun model sedangkan test merupakan data yang dianggap baru dan digunakan sebagai acuan pembanding performa seperti yang dilakukan diatas.
Untuk ide dari regularisasi sendiri muncul dari keadaan seperti pada ilustrasi diatas, yaitu melakukan "penyetelan" pada model yang didapatkan dari data training berdasarkan performanya pada data test. Penyetelan ini sendiri lebih spesifik ke penambahan suatu "penalti" pada fungsi dalam model. Dalam sudut pandang sederhana matematis, penalti ini seakan "mengurangi" nilai parameter (untuk ilustrasi diatas : nilai b1, b2, .., bM pada persamaan polinomial). Tujuan dari penalti ini adalah seperti yang disebutkan sebelumnya : memperoleh model yang walaupun tidak optimal pada data training, memiliki performa lebih baik di data test. Untuk membahas mengenai penerapan regularisasi ini, selanjutnya dibahas 3 jenis regresi yang menggunakan regularisasi : regresi ridge, regresi LASSO, dan regresi elastic net.
Ridge, LASSO, dan Elastic Net
Secara keseluruhan, ketiga jenis regresi ini memberikan penalti dengan cara meningkatkan eroor. Perbedaannya ada pada formula yang digunakan untuk meningkatkan error tersebut. Error pada regresi linear adalah :
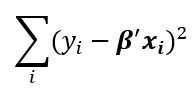
b (beta) merupakan parameter regresi.
Regresi Ridge
Formula error ridge :

λ merupakan koefisien pengali, efeknya adalah mengatur besaran penalti. Koefisien ini juga digunakan di dua model selanjutnya.
Regresi Least Absolute Shrinkage Selector Operator (LASSO)
Formula error lasso :

Kedua model diatas memiliki kelemahan masing-masing. Seperti contoh ridge tidak mengeliminasi variabel yang tidak berguna, sehingga model yang terbentuk cenderung redundant. Sedangkan LASSO cenderung buruk dalam menangani multikolinearitas data karena model ini mengeliminasi variabel yang diidentifikasinya sebagai "mirip" dengan variabel lain. Dari keduanya dibentuk perumuman, dimana bentuk penalti kedua regresi diatas disertakan.
Regresi Elastic Net
Formula error Elastic Net

Untuk membandingkan ketiganya, penulis melakukan hal serupa seperti sebelumnya yaitu melakukan simulasi pada data dummy yang kemudian digunakan untuk membangung ketiga model regresi diatas. Performa ketiga model dibandingkan dengan menggunakan data test dummy, Untuk melakukan simulasi ini pembaca dapat mereplikasi dengan software R dan kode di github penulis : regularisasi .
Sebagai penutup, penerapan regularisasi di machine learning sudah sangat banyak dan tentunya tidak terbatas pada model regresi. Contohnya adalah seperti pada analisis klasifikasi support vector machine (SVM) yang akan penulis bagikan informasinya di masa mendatang.
Akhir kata, harapan penulis setelah pembaca menyelesaikan membaca blog ini adalah agar pembaca setidaknya memahami secara garis besar metode regularisasi dan kelebihan dari model-model regularisasi. Selain itu, agar blog ini bermanfaat bagi pembaca.

Comments